|
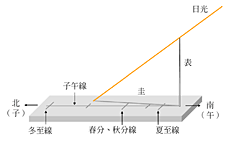
第一章 日圭,也稱為圭臬,又稱為圭表。它是一種利用觀察太陽的投影位置以計算時日、決定節氣的工具,主要由一個垂直的投影物體和一片水平的受影面盤所組成。垂直聳立的投影物體部分,古時稱為「表」,可以小至一塊下方上尖的玉石,中到一根直立的木棍,也可以大至埃及的金字塔。而水平的受影面盤必須大小適中,而面上刻的線條,不論多少,其中不可或缺的是子午線,也就是南北線,以及垂直經過子午線的一些表示節氣的短線,請參考圖1.1。
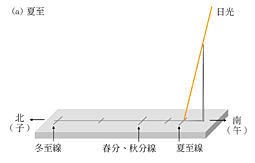
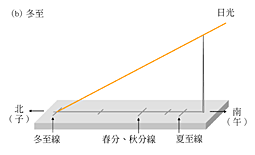
「表」的影子稱為「晷」。隨便哪一天,當「晷」落在子午線上時候,就是那一天的正午。可是在不同的日期,晷頂(標竿影子的頂部)在子午線上的位置不同。請參考圖1.2。那些短線所要指示的,主要是二十四節氣的日期。子午線和那些短線所用到的水平面部分就叫做「圭」。你看它與「圭」字像不像?「立竿見影」這句成語雖指的是成效很快的意思,它和日圭也有分不開的關係。
日圭在中國的歷史上出現很久了。據《史記》記載:黃帝時,派有專人「占日」,那人的名字叫羲和。可能主要工作就是研究太陽的活動,包括運行規律,甚至日蝕、黑子,以卜國運。據《尚書堯典》記載:「期三百有六旬有六日」。就是說那時候的人認為一年有366 天。據《周禮》記載,三千年前西周的周公姬旦在陽城「壘土為圭、立木為表」,設立了圭表。表高約2 米。周公用它測影,確定了一年二十四節氣的日期。周公設計的表是這樣的:上半部是直立的木頭,下半部是土壘成的基座。基座上窄下寬,其斜面的角度是經過設計的,剛好等於當地夏至正午陽光的斜度。因而,在夏至時圭面上是找不到影子的。周公的這個測影台因此而得 了另一個名稱:沒影台。土木做的圭表當然用不久。到了一千二百多年前的唐開元十一年,天文學家在周公測影台舊址上按周公原制,但改土圭為石圭,改木表為石表。這些石製的,現在還保留著,是世界上最古老的天文台遺跡之一。按理說,「表」的頂端應該是直角方形的,好利用那直角邊線做投影邊。但是現在在陽城的唐代的「表」的頂端卻戴上了瓦片,不知是哪個朝代的事? 陽城現在是河南省登封縣告成村。元代的天文家郭守敬在陽城建了一個約有十米高的觀星台。觀星台頂上可以觀星。而觀星台本身也被巧妙地設計成一個大型的「表」。在地面的圭長有17 米。這麼大的一個圭表,使得郭守敬的研究結果領先了西方世界四個世紀之久。相片1.1 和1.2 是台北市天文科教館展出的郭守敬在登封所建的觀星台模型。台頂平台做為觀星用之場地。兩閣樓之間有一橫桿,具有做為日圭之標竿頂點的功用。雖然它在圭上的投影應會因太遠而模糊,但是郭守敬使用景符所以無妨。
相片1.3 是台北市天文科教館展出的一張《欽定書經圖說、卷一、堯典》書裡的「夏至致日圖」,很有意思。表示唐堯時的科學家羲叔在夏至做觀察。畫中小孩和豬、羊、狗都在羲叔旁邊,天上還有飛鳥和太陽。真的很有夏天的味道。可是其中也有一些值得注意的地方:第一,人的衣服是否穿得太多了?尤其是小孩,好像不是夏天。第二,太陽的位置是否太低了?第三,人與物都沒影子。第四、土圭的方向並沒有和太陽的方向配合,也許圖畫並沒有要表示那時是正午。
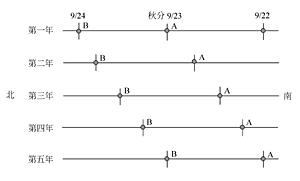
為了符合現代人的口語,日圭裡的「表」,在本書中將用「標竿」來代替。另外,由於經度差以及地球繞日軌道的一些緣故,日圭時間是自然時間,它的正午通常並不是手錶時間的十二點整,因為日圭時間是依太陽位置所定的時間,而手錶時間是為了人類社會行政系統方便而規定的一個人為標準時間。兩者並不一致,所以用手錶時間來討論日圭是不適當的。日圭時間與手錶時間之間需要經過一些補正才能一致。這裡就以經度差的影響為例來說:因為中國全國都以中原標準時間來規定現在是幾點鐘,也就是全國屬於同一標準時區。例如當北京人的手錶顯示是中午12點的同時,昆明人的手錶也顯示是中午12 點。但是因為兩地的經度相差約13 度;雖然兩地的手錶所顯示的時間一樣,太陽的位置可差得很遠。就是當「晷」經過北京市的子午線的時候,太陽離昆明的子午線還有13度的距離。換算成時間,有52 分鐘的差別。顯然,用人為的手錶時間是不適合討論日圭的。因此之故,本書中提及時間時,除非特別交代,都是指日圭時間,以日圭時間的正午為準。日圭時間的正午就是「晷」與子午線合一的時刻,也稱為中天時刻。所以,書裡說中午十二點,指的是日圭上的正午,不是指手錶上的十二點。 日圭有什麼用處?一般人以為日圭只用於觀察節氣日期。其實,日圭可不簡單,它是人類在地面上觀察太陽在天空中運行的科學工具。所以一些地球與太陽之間的關係,也許能從它身上得知一二。古人利用日圭,除了用來分配一天之內的時間,經過長時期的觀察,還獲得了下列科學知識: 一、太陽年的長度 太陽年的長度是地球繞日一周所需的天數。就日圭而言,似乎也是晷頂第二年由同樣方向(由南向北或由北向南)在同樣的時刻回歸到前一次出現的地方所需要的天數。其實不是。以秋分做個例子:若某一年的秋分,就是9 月23 日,那一天正午時晷頂正好落在「圭」的秋分線上。一年若以365 日計,第二年9 月23 日的晷頂會向第一年9 月22 日的刻線方向移動一些。即有遷移現象。當然,第二年9 月24 日的也會向第一年9 月23日的方向移動一些。請參考圖1.3。其中A 和B 分別代表秋分當日和秋分後一日的影子。到了第五年,A 幾乎變成和第一年9 月22 日的刻線重疊了。B 和第一年的秋分的刻線重疊。這時,我們應以9 月24 日做為秋分呢?還是以9 月23 日做為秋分?如果選擇9 月24 日,因為這天的晷頂落在秋分線上;再過四年豈不是得以9 月25 日做為秋分?又再過四年呢?為了避免秋分的日期在日曆上發生移動,羅馬人定下了每四年將二月份的天數增加一天(2 月29 日)的方法。而這方法也被我們沿用到現在。
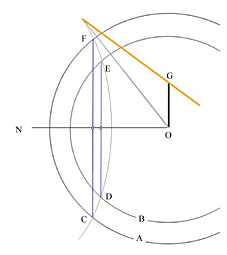
就實驗而言,太陽年長度的基礎在於觀察哪一天是夏至或冬至。以冬至為例,「晷」越來越長就表示越接近冬至。某一天發現「晷」變得比昨天的要短,就說:「昨天是冬至」。此時紀錄下來,這次冬至與上次冬至間的天數差,累積了長期的紀錄,數十年甚至數百年,將這些天數差求出平均值,就得到了平均太陽年長度。若精確度不要求高,只是為了興趣玩一玩,就日圭而言,晷頂滿足同樣方向、同樣時刻和同樣定點約需1461 天。其間地球經過了四個春秋。將1461 除以4,就得到一平均太陽年的長度為365.25 日。 太陽年是自然年。它的長度不是我們人類所能規定或改變的。相對於自然年,我們有人為年,也就是普通所謂的年,它的長度是我們人類所規定的。一人為年有365 或366 日,依是不是閏年而定。一般來說,每四年要閏日一次。嚴格來說,每四年閏日一次並不能長期滿足曆法上的正確性。科學家求得比較精確的平均太陽年長度為365.2422 日。依此數據,應該每四年一閏,百年倍數不閏,四百年倍數要閏,四千年倍數不閏,以便修正。 二、地理上的南北方向線 我們中國人五千年前就用指南針決定南北方向。沒有指南針的民族用什麼呢? 用日圭就可以。 從日出到日沒,晷頂在地面上的移動路線是東西方對稱的。其對稱的軸線就是南北方向線(子午線)。所以只要求出晷的移動對稱軸線,那就是了。其求法是: 1. 在水平面上找好某定點做為原點。如圖1.4 之O 點。以O 點為中心,在水平面上畫出幾個適當半徑的圓弧。如圖1.4 之弧A 和弧B。 2. 在O 點上立起高度適當的標竿OG。OG 不一定要垂直。但若欲利用O 點,則OG 必須與地面垂直。以鉛垂線檢驗垂直。 3. 觀察晷頂的移動,當它與圓弧重疊時,在重疊處做一個記號。每一圓弧有兩次機會遇見頂點影子經過。一次在上午,一次在下午。如圖1.4中之C、D、E 和F。 4. 將每一圓弧的兩個記號點以直線連結,如將圖1.4 中之C 和F 連結,D 和E 連結。CF 和DE 兩線段都是東西方向線,與它們垂直的線就是子午線。
5. 或者求出這些線段的平分線,這些平分線必相互重疊,且通過原點O,如圖中之ON。此平分線就是標竿所在的南北子午線。 另外,可以利用在日圭時間的正午「晷」是南北向的特性,我們若能由手錶知道何時是正午,在那時吊一根鉛垂線來紀錄其影線方向,立刻就得到南北子午線。 三、大地是圓的 「天圓地方」是古代中國人的觀念。「天圓」的觀念由夜裡觀察星星位置的變化方式很容易就有了。「地方」則純粹是假說;並不一定是說大地是「方」形的,而是說除了山巒起伏之外,基本上大地是「平」的。可是這假說經不起日圭的驗證:如果大地是平的,陽光是平行的,為什麼用同樣高的「表」,在同一天,長安的「晷」要比太原的短,比長沙的長?這種長短不一的現象古人一定很早就注意到了。周公為什麼選在陽城立 圭?因為以他當時的地理知識所及,陽城是周國的中心,所以在那兒立圭為準。這種大地是「平」的觀念到了漢武帝時期(西元紀元前一百多年)由洛下閎和耿壽星以及東漢時期的張衡等人推翻。他們提出渾天說,認為天在外,如蛋殼;地在內,如蛋黃。只要承認大地是球形的,在不同的南北緯度上「表」所指的天頂方向不同,與陽光的角度不同;則各地「晷」的長度不同,相互之間並且有一定的數學關係,就成了一件很自然的事請參見圖1.5。
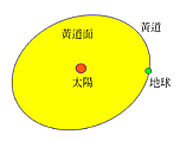
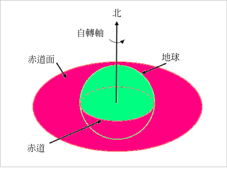
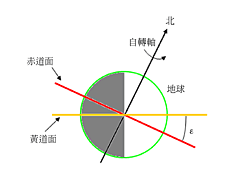
四、黃道面和赤道面的交角 以太陽為中心,地球繞日公轉,一年繞一周。這個繞日軌道叫做黃道。它所形成的面叫做黃道面。請參考圖1.6。 垂直於地球自轉軸又通過地心的面叫做地球的赤道面。請參考圖1.7。
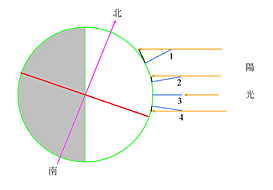
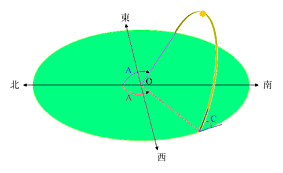
黃道面和地球的赤道面是同一個面嗎?如果是,就代表黃道面與赤道面重疊在一起,也就是地球的自轉軸永遠和太陽光來的方向垂直。如果是這樣,那麼無論地球在黃道上的什麼位置,或者說無論在一年裡的哪一天,地球各地每天接受日照的時間都是12 小時。人們看到太陽永遠在早上六點整由正東方升起,在下午六點整由正西方隱沒。如果是這樣,那麼地球就沒有季節的變化了。但事實上呢? 1. 一年裡有四季變化。也就是說地球表面各地接受日照的時間是隨時日而有變化的。日照時間較長的稱為夏季,較短的為冬季,適中的為春季和秋季。 2. 太陽在地平面出來(或隱沒)的方位角每天不同。請參考圖1.8。每天方位角A(或B)都在變化。以春分和秋分附近日子的變化量最大,以夏至和冬至附近的變化最小。就觀察結果而言,A 與B 的大小非常接近,可以說是相同。 3. 一年裡只有兩天太陽由正東方升起,由正西方隱沒。而這兩天就是春分和秋分。
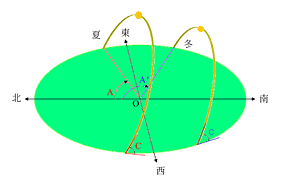
4. 除非我們在在赤道上,太陽絕不以直角角度升起或隱沒。在北半球太陽每天運行的路徑都是斜向南方的。緯度越高斜得越厲害,即圖1.8中之C 角越小。若在南半球,則必斜向北方。 5. 在同一緯度上觀察,不同的日子雖然太陽升起或隱沒的方位角不同,但是它於空中運行路徑的斜度幾乎天天相同。請參考圖1.9,其中冬夏兩個太陽出沒的方位角不同而傾斜角C 角卻相等。(其實∠C =90°–φ。φ(ㄈㄞ)為日圭所在地緯度。)
如何理解這些現象?將地球的自轉軸傾斜一點試試看。只要自轉軸是傾斜的,上述現象都可以得到合理的解釋。自轉軸傾斜了,也就是赤道面傾斜了,那麼黃道面和赤道面就有一個交角。請參考圖1.10。我們把這個交角叫做黃赤交角,用符號ε來代表。
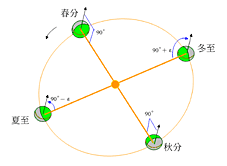
若自轉軸是傾斜的,它和黃道面之間的夾角大小是(90°–ε),那麼地球在黃道上運行,除了兩點以外,自轉軸和太陽光方向都不會垂直。會垂直的那兩個點:一個是春分點,一個是秋分點。請參考圖1.11。
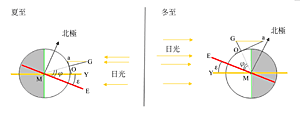
黃道上還有兩個重要的點稱為夏至點和冬至點。地球運行到夏至點的時候,是自轉軸的北極最傾向太陽的時候。那一天地球北極和太陽光方向的夾角是90°–ε。在冬至點的時候,是自轉軸的北極最偏離太陽的時候。那一天地球北極和太陽光方向的夾角是90° +ε。 黃赤交角的大小,即ε的數值,可否在地球上測量?怎麼量? 有日圭,就可以測量ε的大小。 由日圭可以很容易地測得正午太陽離開地平面的角度(仰角)。我們稱此角度為a 角。請參考圖1.12。在夏至時,量得a 角的數值為a1。在冬至時,量得a 角的數值為a2。有了這兩天的數值,ε的大小就可以用下面簡單的式子求出: ε=(a1–a2)÷2
由a1 和a2 的實際測量數值,得ε為23.44°。這也就確定了地球赤道面是以23.44°傾斜於黃道面的11。而66.56°(= 90°–ε)就是地球自轉軸和黃道面之間的夾角,也是北極圈所在的緯度。
|
|||||||||||||||||||||||||||||||||||||||||